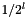NewWave::WaveletCoefficient Class Reference Contains a single wavelet coefficient value, together with its levels. More...
Detailed DescriptionContains a single wavelet coefficient value, together with its levels. The wavelet coefficient has a value, together with the scale information for the wavelet basis function it corresponds to. The scale information is in the form of an integer level, such that the scale is proportional to Definition at line 20 of file WaveletCoefficient.hh. Constructor & Destructor Documentation
Constructor. Construct a WaveletCoefficient from its rapidity level, phi level and value
Member Function Documentation
Give a hash that is unique to the FrequencyBand this coefficient belongs in. The hash is determined by the y-level, the
Give a hash that is unique to the FrequencyBand this coefficient belongs in. The hash is determined by the y-level, the
Is this coefficient part of the "smoothing" coefficients. Depending on the wavelet basis used, some coefficients do not provide any meaningful detail on the decomposition of the signal and can be considered equivalent to the smoothing terms. The 0,0 coefficient is always a smoothing coefficient, but other coefficients may also be included
Return a unique key for the coefficient. In a given event, there is a fixed set of coefficients specifying the event. Each one has a key that is unique within that set. Coefficients from different events may have the same key, of course.
The centre of the The contribution of each coefficient is localised to a region in
The The
The maximum of the The contribution of each coefficient is localised to a region in
The minimum of the The contribution of each coefficient is localised to a region in
Set the value of the coefficient.
The value of the coefficient.
The centre of the The contribution of each coefficient is localised to a region in
The rapidity level of the coefficient. The rapidity level gives the scale of the wavelet basis function in the rapidity axis. The scale is proportional to
The maximum of the The contribution of each coefficient is localised to a region in
The minimum of the The contribution of each coefficient is localised to a region in Friends And Related Function Documentation
Definition at line 186 of file WaveletCoefficient.hh. The documentation for this class was generated from the following file:
Generated on Wed Aug 23 2017 12:59:15 for New Wave - Noise Elimination With Wavelets At Vast Energies by  1.7.6.1
1.7.6.1
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

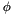 level of the coefficient.
level of the coefficient. 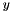 range covered by the coefficient.
range covered by the coefficient. 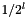 , where
, where 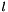 is the level. There are two such levels for rapidity and
is the level. There are two such levels for rapidity and 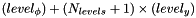
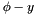 , the size of which depends on the
, the size of which depends on the